
|
|
| . |
Shape-based Feedforward Tuning:
|
||||||||||||||||||||||||||||||||||||||||||
| General Rule of Kaff: | |
|
Notice that in the plot below, the position error plot (white) has a similar shape to the commanded acceleration (yellow), therefore we will add Kaff.
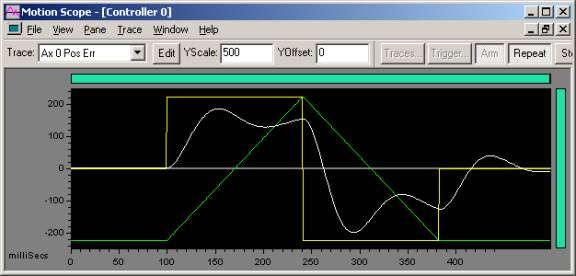 |
||
| 10,000 count move Trapezoidal move: 5e5 accel, decel, vel |
Green - Commanded Velocity Yellow - Commanded Acceleration White - Position Error |
|
|
||
On this stage, adding a Kaff of 1 makes no noticeable difference:
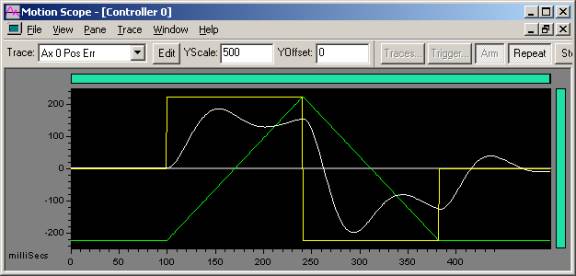 |
||
| 10,000 count move Trapezoidal move: 5e5 accel, decel, vel |
Green - Commanded Velocity Yellow - Commanded Acceleration White - Position Error |
|
|
||
After doubling Kaff each move, we eventually get the following plot when Kaff = 50,000.
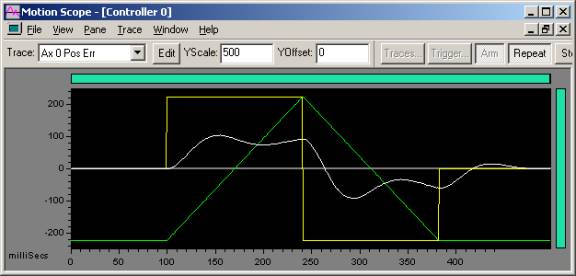 |
||
| 10,000 count move Trapezoidal move: 5e5 accel, decel, vel |
Green - Commanded Velocity Yellow - Commanded Acceleration White - Position Error |
|
|
||
It looks like the position error was roughly reduced by half when we changed Kaff = 50,000. That means that if change the Kaff = 100,000, the position error should be fairly close to zero.
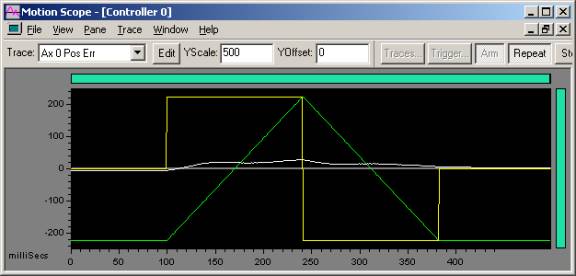 |
||
| 10,000 count move Trapezoidal move: 5e5 accel, decel, vel |
Green - Commanded Velocity Yellow - Commanded Acceleration White - Position Error |
|
|
||
The resulting plot shows a position error that is very close to zero and only has a peak position error of 28 counts—an impressive 85% reduction.
NOTE: This reduction comes with no reduction in stability.
As you can see, adding Kaff (acceleration feedforward) can dramatically reduce position error. The stage is actually more stable because P, I, and D need to deal with smaller disturbances, while Kaff is doing most of the work.
Obviously, for the example above, we found a good value for Kaff rather quickly. To see some additional plots with different Kaff values (for the same commanded move) to show that the shape pattern of Kaff is fairly simple and consistent, click here.
| | | Copyright © 2001-2021 Motion Engineering |